Measuring Your World: Dp Update (Part One)
Sine
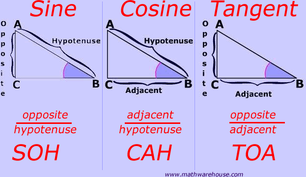
Sine is a trigonemtric feature that is equal to the ratio of the side opposite of a angle.
Sine was commenly used using a caculator to find a length on different shapes or
triangles and when use on a caculator would speed up the process.
Cosine
Cosine was the trigonometric feature that was equal to the ratio of a side adjacent to a angles like the acute angle.
Cosine was also commenly used on a caculator and when used on a caculator could speed up the process for myself
and thats where I most commenly used it and learned using it.
Tangent
Tangent is a straight line that is touches a curved line or shape at a instance but cannot cross though the shape or curve.
The Tangent was commenly used when trying to find a direction of a certain point in between the structure I was working
with at the time. A Tangent will always have the same direction as the curve that the point is on.
Sine
Sine is a trigonemtric feature that is equal to the ratio of the side opposite of a angle.
Sine was commenly used using a caculator to find a length on different shapes or
triangles and when use on a caculator would speed up the process.
Cosine
Cosine was the trigonometric feature that was equal to the ratio of a side adjacent to a angles like the acute angle.
Cosine was also commenly used on a caculator and when used on a caculator could speed up the process for myself
and thats where I most commenly used it and learned using it.
Tangent
Tangent is a straight line that is touches a curved line or shape at a instance but cannot cross though the shape or curve.
The Tangent was commenly used when trying to find a direction of a certain point in between the structure I was working
with at the time. A Tangent will always have the same direction as the curve that the point is on.

The ArcSin (Sine/Cosine/Tangent)
ArcSine
ArcSine is the inverse version of a sine function the only difference is formulas. Arcsine was used on a majority of triangle angles and required alittle bit of information before plugging into a caculator or doing the formula. I am still alittle confused on how the "Arc" functions work although they are starting to make more sense as Learn more about them.
ArcCosine
Arc Cosine is also the inverse version of the actual cosine function. Once again the only difference is formulas and of course
the way you are going to use it with different shapes and in a caculator or doing it on paper.
ArcTangent
Arc Tangent is similar like the rest of the Arc's its the inverse version of Tangent, and once again the only difference is how
you write the sin signs down. The tangent is asking you to find the inverse tan slope (y/x). The way I figure this out was after
learning about it in class I went and learned more about it on khan academy and that really helped me have a more
confident understanding of ArcTangent.
Law os Sin (Sines and Cosines)
Law of Sines
The law of signs is trigonometry at least is a sine formula or rule in the form of a equation with the lengths of the sides of a
triangle to the sines of its angles. ( Sin(A) = Sin(B) = Sin(C) ). Usually Labeled on the triangle on each sides or inside corners.
The law of sines were uswed for finding the lengths of the sides of a triangle (any shape) to the sines of its angles. It can also
be used when two sides and one non-enclosed angles are known.
Law of Cosines
the law of cosines is the relationships of letters in between the triangle or whatever shape your using. In a case of a triangle there would
be multiple sets of different letters. The sets of letters have relationships together. There is also a formula to be used using these letters. I remember using law of cosines a lot when you don't know where to start so you just start labeling around to find a start.
Major Steps in learning
Using the Pythagorean Theorem to derive the Distance Formula
The Distance Formula and Pythagorean Theorem are very similar except Distance Formula is alittle different than Pythagorean Theorem and is Basically Pythagorean Theorem is disguise. To caculate the distance between the two points A and B you gotta use the Pythagorean Theorem's formula. First draw a right triangle which will have the segment AB as its hypotenuse. If the lengths of the sides are a and b, then by the Pythagorean Theorem, (AB)^2 = (AC)^2 + (BC)^2. Solving for the distance AB, we have AB = (square root)(AC)^2 + (BC)^2. The way I remember learning this is showing us the Pythagorean Theorem at the end of glass and then slowely contributing it into our work.
Using the Distance Formula to derive the equation of a circle centered at the origin of a Cartesian coordinate plane
The distance formula was used with the Cartesian coordinate plane very commonly and was very confusing to find out especially because the distance formula was hard to understand in the first place. The distance formula is the same thing at the Pythagorean Theorem except mortified a little bit and a Cartesian coordinate plane is specific points uniquely in a plane by a pair of numbered coordinates.
Defining the Unit Circle
The unit circle is a circle with a radius of one. Frequently, especially in trigonometry, a unit circle is the radius of one centered at the orgin (0,0) of a circle or Cartesian coordinate system. The Unit circle was used as a example for a lot of things and I noticed that we would almost everyday draw a unit circle to learn another formula on it or another way to caculate a point of something in that interest. The unit circle is the starting point of all of these functions.
Finding points on the unit circle (at 30 degrees, 45 degrees and 60 degrees)
The way I learned is using the formula to find the right number for each section within the unit circle and then after that you would take the degrees then find the side that is adjacent to the 30 degree angle, lets say it on the left therefore the corresponding side on the triangle on the right has to be half that. This was a simple concept you needed to know to do functions. Using a unit circle although was not use for everything is was pretty useful to know to continue with the rest of the functions.
Using the symmetry of a circle to find the remaining points on the unit circle
This was another concept that was hard for me to figure out but after awhile it became simplier and after some pratice you could do it
without a lot of mistakes it was just a matter of knowing what to do and to not forget any steps or the main formulas to figure
everything out.
Using the unit circle to define sine and cosine (of the angle theta)
Sine and Cosine can be used on a unit circle. Sine and Cosine are like functions on the Unit circle. First you draw a unit circle, centered with the origin and a radius of one. Separate the x and y axes into coordinate plane into four quarters. Then label the four quadrants. Then this means x = cos t and y = sin t. I had difficulty on this one and don't know the full way of doing it but I do know some parts of how to use a unit circle with sine and cosine so this was what I could think of.
Defining the tangent function
Tangent function is once again another type of formula and can be used in many ways. Tangent is a main function in Trigonometry and they are based of of Right-Angled Triangle. The Tangent function is a periodic function which is very important in trigonometry. The way tangent function is used is on a unit circle. There is a lot that can be used by the tangent function. I remember using this function on the caculator two and learning about this being a major part of trigonometry in class.
Using similarity and proportions to derive the general trigonometric functions (sine, cosine and tangent)
All three of these trigonometric functions were pretty similar and once you learned the simple concept after that you learned about
each of the different trigonometry features and it was all down hill there. All you had to do was know the difference between all three and you
would be set although I did get confused from a lot of them after you figure them all out your good to go. All three of these were similar is some way.
Using the unit circle to define the arcSine, arcCosine and arcTangent functions
The unit circles are used a lot to describe what ArcSine, ArcCosine and ArcTagents are so its pretty obvious what they are used for thoughout
the community of trigonometry. The learning of each of these functions with unit circles was pretty easy once you learned how to use unit circles
because after that it just was a matter of figuring out different way of using these types of functions thoughout the unit circle.
Using the Mount Everest problem to discover the Law of Sines ("taking apart")
The Law of Sines is already in the Mount Everest problem or you can add it you have a triangle with a, b, and c. Law of sines is the
relationships between a capital A and a lower case a in between the triangles. So you could use the Law of Sines relationships and the
Law of Sines formula to get closer to the answer or using them to start it unless you have some information to plug it in.
Deriving the Law of Sines
Law of sines in trigonometry, is the equation relating to the lengths of the sides of a any shaped triangle to the sines of its angles. The law of sines was used a lot in labeling and making things more organized and the formula was also used a lot to find points on a triangle. This was used a lot throughout our worksheets.
Deriving the Law of Cosines
Law of Cosines is useful for finding the third side of a triangle. It was also very useful once again for labeling different section at the beginning of starting any triangle problem. The law of Cosines formula was pretty popular throughout the course and was used to solve different types of triangles like the SSS triangle.
Using the Pythagorean Theorem to derive the Distance Formula
The Distance Formula and Pythagorean Theorem are very similar except Distance Formula is alittle different than Pythagorean Theorem and is Basically Pythagorean Theorem is disguise. To caculate the distance between the two points A and B you gotta use the Pythagorean Theorem's formula. First draw a right triangle which will have the segment AB as its hypotenuse. If the lengths of the sides are a and b, then by the Pythagorean Theorem, (AB)^2 = (AC)^2 + (BC)^2. Solving for the distance AB, we have AB = (square root)(AC)^2 + (BC)^2. The way I remember learning this is showing us the Pythagorean Theorem at the end of glass and then slowely contributing it into our work.
Using the Distance Formula to derive the equation of a circle centered at the origin of a Cartesian coordinate plane
The distance formula was used with the Cartesian coordinate plane very commonly and was very confusing to find out especially because the distance formula was hard to understand in the first place. The distance formula is the same thing at the Pythagorean Theorem except mortified a little bit and a Cartesian coordinate plane is specific points uniquely in a plane by a pair of numbered coordinates.
Defining the Unit Circle
The unit circle is a circle with a radius of one. Frequently, especially in trigonometry, a unit circle is the radius of one centered at the orgin (0,0) of a circle or Cartesian coordinate system. The Unit circle was used as a example for a lot of things and I noticed that we would almost everyday draw a unit circle to learn another formula on it or another way to caculate a point of something in that interest. The unit circle is the starting point of all of these functions.
Finding points on the unit circle (at 30 degrees, 45 degrees and 60 degrees)
The way I learned is using the formula to find the right number for each section within the unit circle and then after that you would take the degrees then find the side that is adjacent to the 30 degree angle, lets say it on the left therefore the corresponding side on the triangle on the right has to be half that. This was a simple concept you needed to know to do functions. Using a unit circle although was not use for everything is was pretty useful to know to continue with the rest of the functions.
Using the symmetry of a circle to find the remaining points on the unit circle
This was another concept that was hard for me to figure out but after awhile it became simplier and after some pratice you could do it
without a lot of mistakes it was just a matter of knowing what to do and to not forget any steps or the main formulas to figure
everything out.
Using the unit circle to define sine and cosine (of the angle theta)
Sine and Cosine can be used on a unit circle. Sine and Cosine are like functions on the Unit circle. First you draw a unit circle, centered with the origin and a radius of one. Separate the x and y axes into coordinate plane into four quarters. Then label the four quadrants. Then this means x = cos t and y = sin t. I had difficulty on this one and don't know the full way of doing it but I do know some parts of how to use a unit circle with sine and cosine so this was what I could think of.
Defining the tangent function
Tangent function is once again another type of formula and can be used in many ways. Tangent is a main function in Trigonometry and they are based of of Right-Angled Triangle. The Tangent function is a periodic function which is very important in trigonometry. The way tangent function is used is on a unit circle. There is a lot that can be used by the tangent function. I remember using this function on the caculator two and learning about this being a major part of trigonometry in class.
Using similarity and proportions to derive the general trigonometric functions (sine, cosine and tangent)
All three of these trigonometric functions were pretty similar and once you learned the simple concept after that you learned about
each of the different trigonometry features and it was all down hill there. All you had to do was know the difference between all three and you
would be set although I did get confused from a lot of them after you figure them all out your good to go. All three of these were similar is some way.
Using the unit circle to define the arcSine, arcCosine and arcTangent functions
The unit circles are used a lot to describe what ArcSine, ArcCosine and ArcTagents are so its pretty obvious what they are used for thoughout
the community of trigonometry. The learning of each of these functions with unit circles was pretty easy once you learned how to use unit circles
because after that it just was a matter of figuring out different way of using these types of functions thoughout the unit circle.
Using the Mount Everest problem to discover the Law of Sines ("taking apart")
The Law of Sines is already in the Mount Everest problem or you can add it you have a triangle with a, b, and c. Law of sines is the
relationships between a capital A and a lower case a in between the triangles. So you could use the Law of Sines relationships and the
Law of Sines formula to get closer to the answer or using them to start it unless you have some information to plug it in.
Deriving the Law of Sines
Law of sines in trigonometry, is the equation relating to the lengths of the sides of a any shaped triangle to the sines of its angles. The law of sines was used a lot in labeling and making things more organized and the formula was also used a lot to find points on a triangle. This was used a lot throughout our worksheets.
Deriving the Law of Cosines
Law of Cosines is useful for finding the third side of a triangle. It was also very useful once again for labeling different section at the beginning of starting any triangle problem. The law of Cosines formula was pretty popular throughout the course and was used to solve different types of triangles like the SSS triangle.
Measuring Your World (Part Two)
Introduction and Overview:
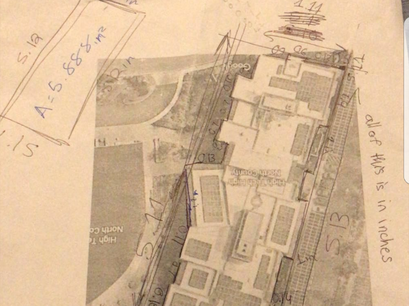
We decided to measure High tech High, we wanted to measure a building where we always had access. School seemed like the perfect solutions for our measurements. To obtain the measurements me and max (1 of my group partners) decided to split up the measurements so both of us could get this part of the math out of the way. I measured High Tech High with a ruler and then later converted it into a more accurate measurements although max did most of the converting once I found the measurements. To make sure that everything was accurate we went back and measured each wall heading in the one direction to make sure it was accurate.
Mathematical Process:
The way we found the measurements, is taking a ruler and a printed out picture of High tech High, we used a ruler to measure each wall of High Tech High and converted the inches from the ruler into a more realistic measurements (feet) and than we measured it again to make sure we got all the measurements correctly. The formula's we used A*Tan(T)=O to find the height using the Tan Function and eventually find the volume. To find the volume we used all of the calculations we had and brought it together to find the total volume.
Reflection:
The project went well, although I think we should've had more time to create a presentation and more time to find the calculations because a lot of the time we had to work on this project at home which was hard to communicate to each other because everyone has their own agenda. A challenge was finding a formula for the measurements of the building. A Habits of a Mathematician that we used was collaborating and listening. Many of us were gone and not available all at the same time so we had to work. Something I would do differently is get the measurements done earlier and try to get in a group sooner. We would just be faster too the hard parts so we can get the easier parts done.
Introduction and Overview:
We decided to measure High tech High, we wanted to measure a building where we always had access. School seemed like the perfect solutions for our measurements. To obtain the measurements me and max (1 of my group partners) decided to split up the measurements so both of us could get this part of the math out of the way. I measured High Tech High with a ruler and then later converted it into a more accurate measurements although max did most of the converting once I found the measurements. To make sure that everything was accurate we went back and measured each wall heading in the one direction to make sure it was accurate.
Mathematical Process:
The way we found the measurements, is taking a ruler and a printed out picture of High tech High, we used a ruler to measure each wall of High Tech High and converted the inches from the ruler into a more realistic measurements (feet) and than we measured it again to make sure we got all the measurements correctly. The formula's we used A*Tan(T)=O to find the height using the Tan Function and eventually find the volume. To find the volume we used all of the calculations we had and brought it together to find the total volume.
Reflection:
The project went well, although I think we should've had more time to create a presentation and more time to find the calculations because a lot of the time we had to work on this project at home which was hard to communicate to each other because everyone has their own agenda. A challenge was finding a formula for the measurements of the building. A Habits of a Mathematician that we used was collaborating and listening. Many of us were gone and not available all at the same time so we had to work. Something I would do differently is get the measurements done earlier and try to get in a group sooner. We would just be faster too the hard parts so we can get the easier parts done.